Pour comprendre et exploiter les ressources d’énergie géothermique, les données et les cartes géoscientifiques sont cruciales. L’une des technologies qui permettent aux ingénieurs de créer des cartes avec des structures géologiques et des types de roches est le geosteering : les mesures électromagnétiques acquises par un instrument d’enregistrement de forage équipé d’émetteurs et de récepteurs sont interprétées et la structure géologique du sous-sol est cartographiée. L’interprétation des données expérimentales est, d’un point de vue mathématique, un problème inverse, qui consiste à évaluer des paramètres spécifiques d’une équation aux dérivées partielles à partir de mesures données. Le résoudre par des méthodes traditionnelles est très coûteux sur le plan informatique.
Dans le cadre du projet PIXIL, et en collaboration avec le Barcelona Supercomputing Center, l’équipe du BCAM vise à intégrer des algorithmes de Deep Learning (DL) dans la résolution de ces problèmes. Les méthodes DL sont rapides, mais nécessitent un ensemble de données de formation massif. Cet ensemble est essentiel pour l’estimation couche par couche des modèles terrestres inversés, qui peuvent être utilisés pour les ajustements en temps réel de la trajectoire du puits pendant les opérations de geosteering.
Dans ce contexte, nous avons récemment développé une stratégie pour générer des bases de données massives qui relient plusieurs modèles terrestres aux mesures de résistivité de forage correspondantes. Pour cela, nous discrétisons une formulation variationnelle 2,5D des équations de Maxwell : nous utilisons des fonctions de base polynomiales et nous adoptons une analyse isogéométrique raffinée. Ce mécanisme de raffinement consiste à réduire la continuité de la solution localement, tout en conservant une distribution optimale des ressources de calcul. Bien que cette stratégie augmente la taille du problème, elle décompose intelligemment la structure de la matrice de rigidité, ce qui entraîne une réduction du solveur direct par un facteur allant jusqu’à 50, par rapport aux discrétisations isogéométriques traditionnelles.
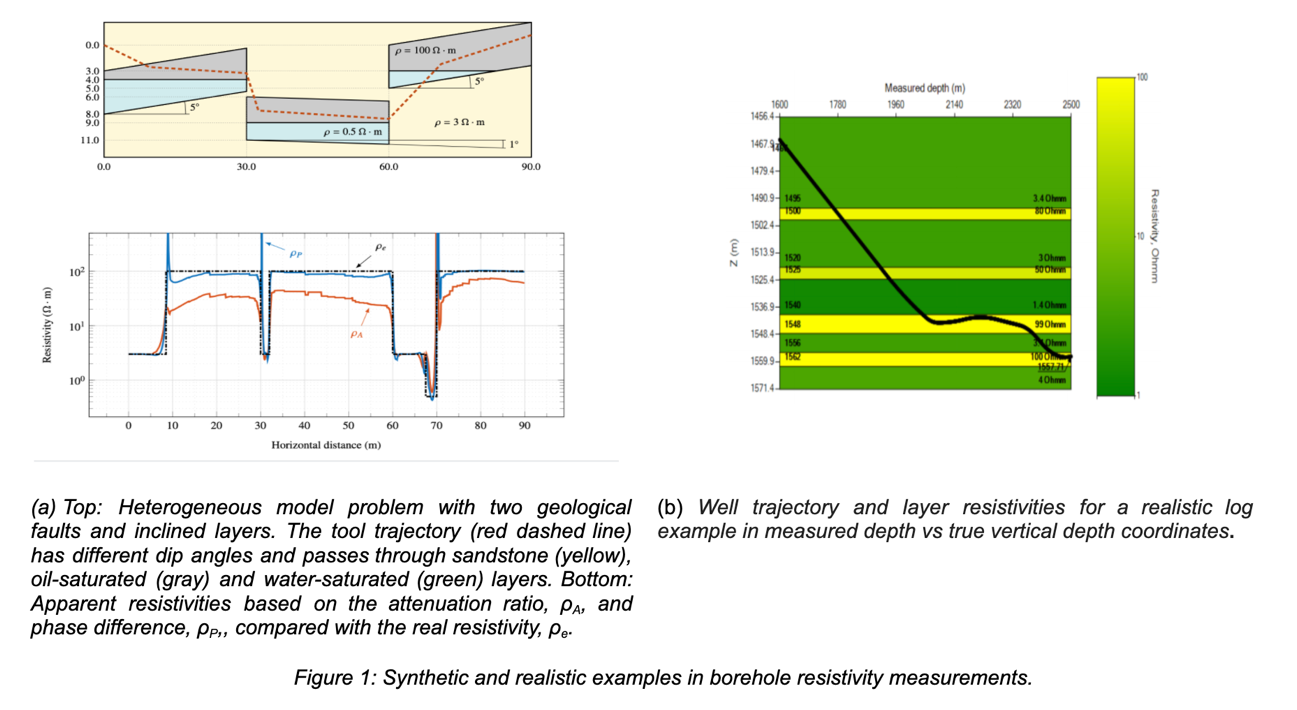
Pour créer un jeu de données pour l’inversion du deep learning, nous avons d’abord sélectionné certains paramètres de discrétisation en fonction des résultats de plusieurs solutions homogènes. Ensuite, nous avons vérifié la précision sur des supports homogènes et hétérogènes. Dans la figure 1a, nous montrons un problème de modèle hétérogène avec deux failles géologiques et couches inclinées (en haut), et les résistivités exactes et numériques (en bas).
Enfin, nous avons généré une base de données synthétiques significative composée de 100 000 modèles terrestres avec les mesures correspondantes en environ 56 heures à l’aide d’un poste de travail équipé de deux processeurs. Ici, par base de données synthétiques significative, nous entendons un ensemble de mesures de forage qui couvre des plages adéquates de variation des variables impliquées (c’est-à-dire des modèles de paramétrage de la Terre) et devrait être suffisant pour une inversion DL robuste. La figure 1b illustre la trajectoire du puits et les résistivités des couches pour un exemple de logarithme réaliste en profondeur mesurée par rapport aux coordonnées de profondeur verticale réelles.
Les travaux futurs comprennent la prise en compte de modèles de la Terre avec de multiples failles géologiques et la complémentarité de la base de données synthétiques par des modèles réels de la Terre, ainsi que des paramétrages plus complexes des modèles de la Terre, par exemple des couches anisotropes.