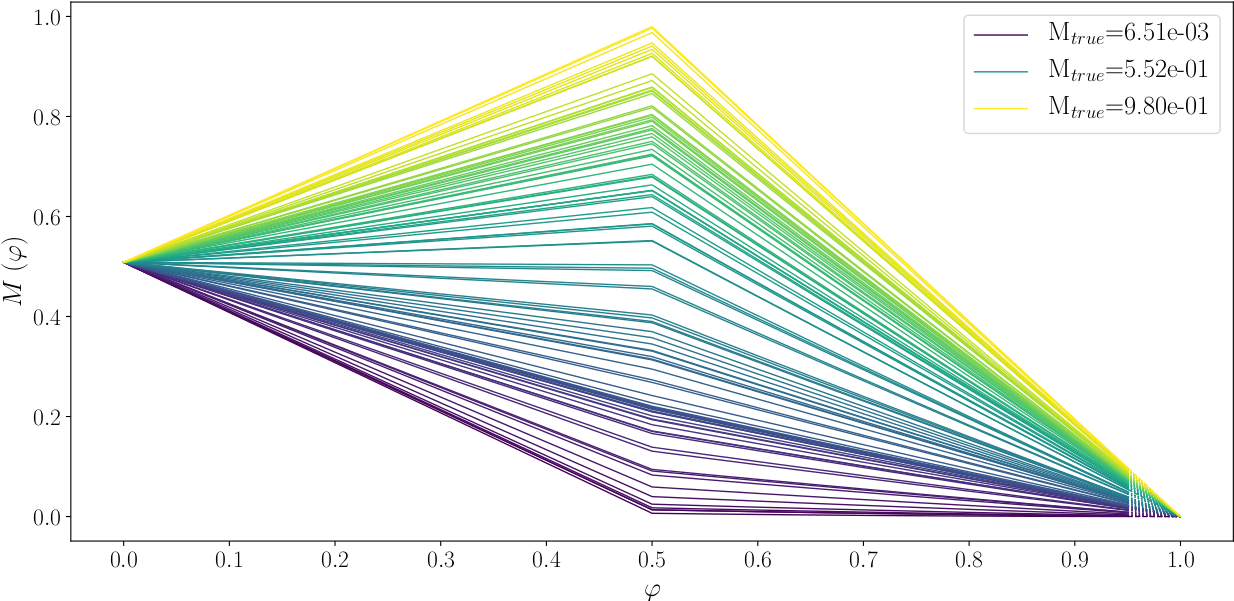
Figure 1 : Construction d’une série de modèles de vitesse M(φ). Chaque courbe montre l’évolution d’une valeur de vitesse unique en fonction de φ. Le modèle a tendance à être homogène (la même valeur de vitesse partout) car φ approche 0 ou 1 et les évolutions sont linéaires sur les deux segments. Les valeurs du modèle de vitesse réelle sont trouvées sous φ =0,5.
Dans une précédente newsletter sur l’inversion complète de forme d’onde (FWI) sur les ondes de surface, nous avons montré une étude préliminaire avec des données réelles (jeu de données "Seignosse”) fournies par RealTimeSeismic. Nous avons conclu que davantage d’efforts devraient être déployés pour faire correspondre la simulation et les données réelles. Nous avons souligné la nécessité d’un examen de la fonction coût en raison des caractéristiques des ondes de surface. La fonction coût actuelle dans le code Hawen est construite dans le domaine fréquence-espace (FX) tandis que de nombreuses articles suggèrent fortement une formulation dans le domaine du nombre d’ondes- fréquence (FK) pour les ondes de surface. Par conséquent, nous avons comparé les deux fonctions coût calculées sur une série de modèles de vitesse M(φ). Nous avons le vrai modèle lorsque φ= 0,5.
La Figure 1 montre l’évolution des modèles de vitesse en fonction de φ. Nous sommes partis d’un modèle homogène avec une valeur de vitesse intermédiaire et avons terminé par un autre modèle homogène présentant une faible vitesse. Il y avait 28 modèles en tout. Une simulation directe comportant des dizaines de fréquences est effectuée pour chacune d’entre elles, et le résultat est comparé à la simulation de référence réalisée avec la vraie modèle. Nous avons mesuré leur distance euclidienne dans les domaines FX et FK respectivement. Les courbes fonction coût pour chaque fréquence et pour tous les modèles de vitesse sont affichées dans la Figures 2 a et c montrent l’évolution de la fonction coût calculée dans le domaine FX ; b et d montrent leur évolution dans le domaine FK. Les figures 2 c et d mettent en évidence la tendance des fonctions de coût proches du modèle réel.
En général, la fonction coût diminue de manière monotone pour les hautes fréquences à mesure que le modèle approche la vraie (au moins sur la moitié gauche des courbes). Dans le cas des basses fréquences, la tendance est plus compliquée : la Figure 2 a indiqué que l’inversion pourrait stagner à environ φ=0,3 si l’on commençait le FWI à partir de la moitié gauche dans le domaine FX; La Figure 2 b montre que la FWI pourrait aller plus loin aux basses fréquences dans le domaine FK malgré les oscillations après φ=0,4. La moitié droite des courbes indique des conditions défavorables pour la FWI: les courbes sont presque plates lorsqu’elles sont φ>0,7, et augmentent à mesure que φ approche 0,5 pour les basses fréquences. Cela indique que nous avons intérêt à commencer une FWI à partir de modèles homogènes présentant de faibles estimations de vitesse. La Figure 2 d met en évidence l’avantage majeur de la fonction coût dans le domaine FK par rapport à celle du domaine FX illustrée en Figure 2 c : le « bassin d’attraction » est plus grand et plus lisse dans le domaine FK, ce qui est une condition favorable à la convergence du résultat FWI vers le meilleur modèle.
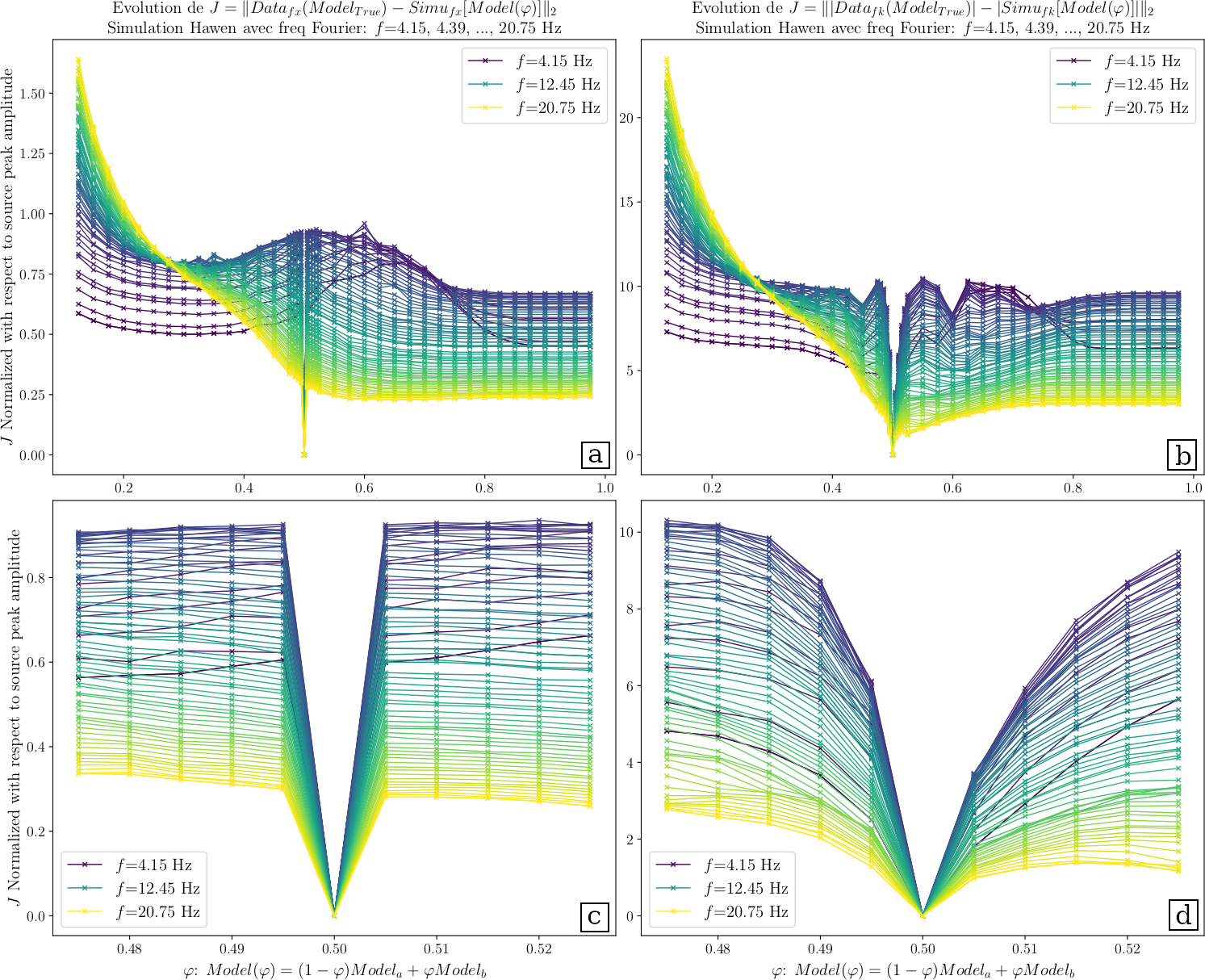
Figure 2 : Courbes de fonction de coût calculées pour une série de modèles de vitesse M(φ). Chaque courbe montre l’évolution d’une fonction de coût en fonction de φ, à savoir un modèle de vitesse donné. Figure 2 a et c correspondent à la fonction de coût construite dans le domaine FX tandis que Figure 2 b et d dans le domaine FK. Les Figures 2 c et d mettent en évidence la partie centrale des Figures 2 a et b, où les modèles sont proches du modèle réel. Il est évident que le « bassin d’attraction », à savoir la vallée près de φ = 0,5, est plus grand et plus lisse dans le domaine FK.
En conclusion, le domaine FK est potentiellement le domaine le plus approprié pour une FWI présentant de fortes ondes de surface, car la fonction coût montre un « bassin d’attraction » plus grand et plus lisse. Nous avons construit une nouvelle fonction de coût dans le domaine FK et la testons actuellement avec des données synthétiques.