To understand and exploit geothermal energy resources, geoscientific data and maps are crucial. One of the technologies that allow engineers to create maps with geological structures and rock types is geosteering: electromagnetic measurements acquired by a drilling logging instrument equipped with transmitters and receivers are interpreted and the geological structure of the subsurface is mapped. The interpretation of the experimental data is, from a mathematical point of view, an inverse problem, which consists in evaluating specific parameters of a partial differential equation from given measurements. Solving it through traditional methods is computationally very expensive.
As a part of the PIXIL project, and in collaboration with Barcelona Supercomputing Center, BCAM team aims at incorporating Deep Learning (DL) algorithms in the resolution of these problems. DL methods are fast, but require a massive training dataset. This is essential for layer-by-layer estimation of the inverted Earth models, which may be used for real-time adjustments of the well trajectory during geosteering operations.
In this context, we have recently developed a strategy to generate massive databases that relate multiple Earth models with the corresponding borehole resistivity measurements. For this, we discretize a 2.5D variational formulation of Maxwell’s equations: we use polynomial basis functions and we adopt refined isogeometric analysis. This refining mechanism consists of reducing the continuity of the solution over local areas of the domain, while keeping an optimal distribution of computational resources. Although this strategy increases the problem size, it also breaks the structure of the stiffness matrix properly, which results in a reduction in the direct solver of up to 50, with respect to traditional isogeometric discretizations.
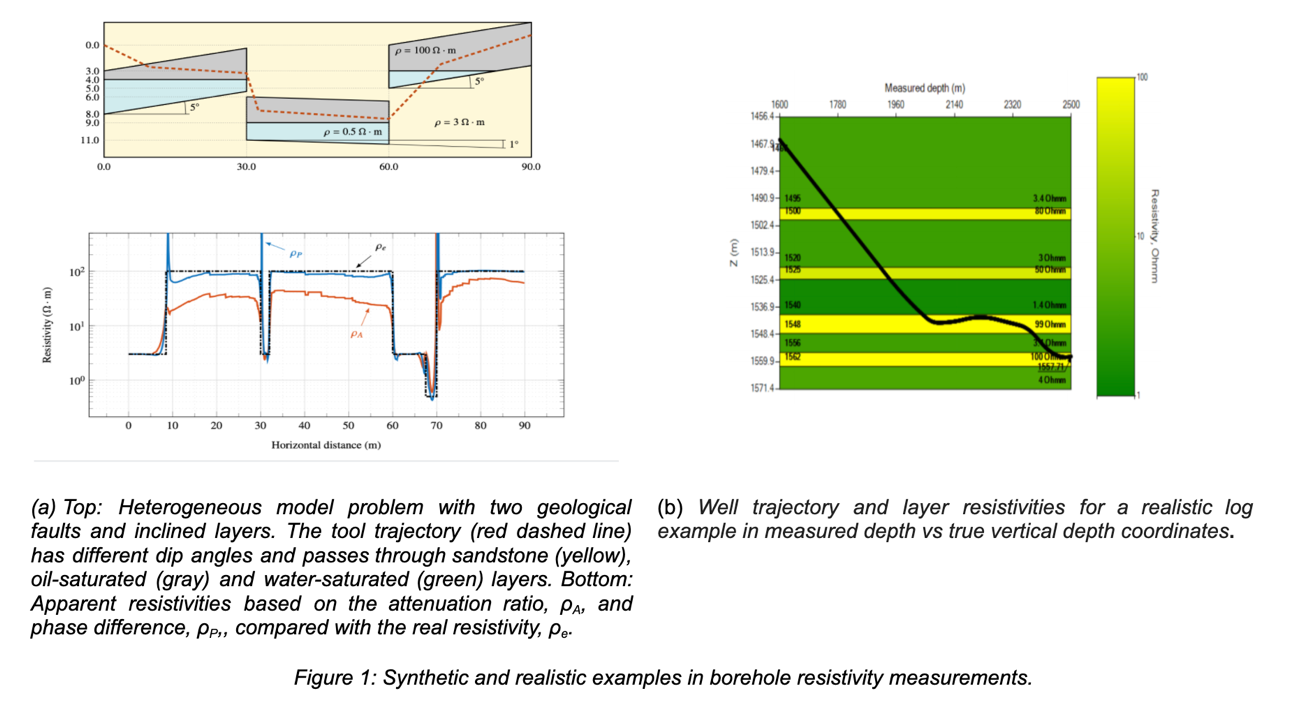
To create a dataset for deep learning inversion, we first selected certain discretization parameters based on the results of several homogeneous solutions. Then, we checked the accuracy over homogeneous and heterogeneous media. In Figure 1a, we show a heterogeneous model problem with two geological faults and inclined layers (top), and the exact and numerical resistivities (bottom).
Finally, we generated a meaningful synthetic database composed of 100,000 Earth models with the corresponding measurements in about 56 hours using a workstation equipped with two CPUs. Herein, by meaningful synthetic database we mean a set of borehole measurements that covers adequate ranges of variation of the involved variables (i.e., Earth parameterization models) and should be sufficient for a robust DL inversion. Figure 1b depicts the well trajectory and layer resistivities for a realistic log example in measured depth vs true vertical depth coordinates.
Future works include considering Earth models with multiple geological faults, and complementing the synthetical database with real Earth models, along with more complex Earth model parameterizations including anisotropic layers.